-

-
Accurion EP4 成像椭偏仪

- 品牌:Park原子力显微镜
- 型号: Accurion EP4
- 产地:亚洲 韩国
- 供应商报价:面议
-
Park原子力显微镜公司
 更新时间:2024-04-08 10:16:50
更新时间:2024-04-08 10:16:50 -
销售范围售全国
入驻年限第10年
营业执照已审核
- 同类产品成像光谱椭偏仪(2件)

立即扫码咨询
联系方式:400-8226768
联系我们时请说明在仪器网(www.yiqi.com)上看到的!
扫 码 分 享 -
为您推荐
- 1
详细介绍
- Accurion EP4成像椭偏仪

Accurion EP4
成像椭偏仪
EP4是新一代的成像椭偏仪,它有机地结合了传统光谱椭偏仪和光学显微镜技术。这使得我们能够在小至1µm的微结构上以椭偏仪的灵敏度表征薄膜厚度和折射率。显微镜部分能够同时测量光学系统全视场范围内的所有结构。传统的椭偏仪注重于测量整个光斑,而不能实现高精度的横向分辨率,并且需要逐点测量。
EP4的显微镜功能使得我们能够获得微观结构的椭偏增强对比图像。在相机的实时图像中可以看到折射率或厚度的微小变化。允许识别椭偏测量的感兴趣区域(选区测量),以获得厚度(0.1 nm-10µm)和折射率的值。单次测量就可以获取厚度和折射率横向变化的3D图。
各种联用技术,例如原子力显微镜(AFM)、石英晶体微天平(QCM-D)、反射式测量仪、拉曼光谱仪等等,可以对同一区域进行原位分析。
另有在各种受控温度和气氛环境下测量的附件可选。
主要功能
模块化配置:从布鲁斯特角显微镜、单波长成像椭偏仪、多波长成像椭偏仪、全光谱成像椭偏仪,在不同配置之间可轻松升级。
波长范围190/250/360nm至1000/1700/2700 nm的光谱成像椭偏仪
横向分辨率低至1um,可测量小至1um的微结构的厚度和折射率
用于样品实时可视化观测的椭偏增强对比度图像
先图像识别样品,然后再测量:在实时视场中直观地选择测量区域(选区测量)
所选视场内多个区域(多个选区)的平行测量
光斑切割技术,消除椭偏测量的背底反射
多种附件可选,如电化学池、温度控制或液体处理样品池,满足多种测量需求
质量控制:提供OEM版本用于产品线中的质量控制

技术
成像椭偏技术(IE)
Accurion成像椭偏仪将椭偏仪和光学显微镜的优点有机地结合在一起。这两种技术的统一创造了一种特有的计量工具,它重新定义了椭偏仪和偏光显微镜。成像椭偏仪增强的空间分辨率(约1µm)将椭偏测量扩展到微观分析、微电子和生物分析的新领域。
成像椭偏法简介
成像椭偏法是一种全光学、非接触式测量技术,适用于微结构薄膜样品和基底样品的膜层厚度测量和材料表征。
该技术将显微镜成像与光谱椭偏测量技术相结合。使空间分辨率达到1µm,轻松突破了传统椭偏仪、反射仪等其他光学测量工具的极限。
椭偏测量的原理是基于样品与偏振光的相互作用。测量获得的偏振参数通过计算建模转化为样品的物理特性图像,如膜层厚度、折射率和吸收系数、粗糙度或各向异性等数据。
什么是成像椭偏技术?
成像椭偏技术结合了光学显微镜和椭圆偏振技术,可针对微结构薄膜和基底进行空间分辨层的厚度和进行折射率的测量。它是一种基于样品与偏振光相互作用的全光学、无损测量技术。它对单层和多层超薄膜有着高度的敏感性,范围从单原子或单分子层(亚纳米范围)到几微米的厚度。
成像椭偏仪可生成测量的图像。最突出的例子是层厚度图,其中每个图像像素都是测量的厚度值。(图 1)。
成像椭偏仪以低至 1 µm 的空间分辨率进行层厚度测量,轻松突破传统椭偏仪的分辨率限制。不需要紧密的光束聚焦就能够达到这种分辨率,并提供样品的空间信息(例如层厚度分布),而无需在此过程中移动和扫描样品。
显微镜和椭偏法的结合还可以检测图像实时视图中已有的薄膜厚度和折射率的微小变化,而无需运行完整的椭偏测量(图2)。这种椭偏对比增强显微镜 (ECM) 拥有非常快速且稳定的性能,用于快速测绘应用中的定性薄膜分析、质量控制和缺陷检测。
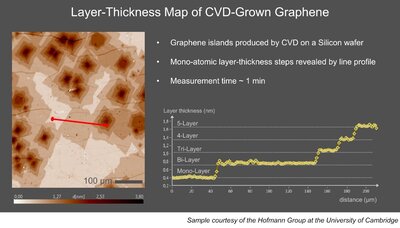 图1:成像椭偏仪的应用示例
图1:成像椭偏仪的应用示例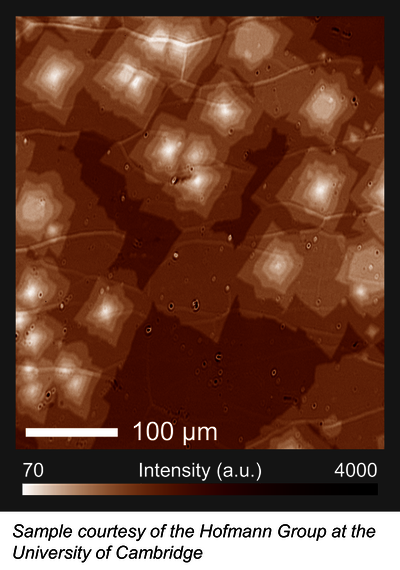 图 2:硅晶圆上 CVD 生长的多层石墨烯岛的椭偏对比图像(ECM 图像)。
图 2:硅晶圆上 CVD 生长的多层石墨烯岛的椭偏对比图像(ECM 图像)。与传统的椭偏技术相比,成像椭偏技术有什么优点?
成像椭偏仪的空间分辨率低至 1 µm,轻松突破传统椭偏仪的分辨率限制。
单次测量即可创建包含超过 500000 个点的二维图。 传统的椭偏仪需要扫描并移动样品来测量二维平面图。
固有的椭圆偏振增强显微镜 (ECM) 可以非常快速地检测薄膜厚度和折射率变化,而无需运行完整的椭圆偏振测量。
“先查找,后测量”。成像椭偏仪的图像实时视图可帮助您在椭偏测量之前识别感兴趣的相关样品位置。它甚至显露微小的表面修饰,包括亚纳米厚度台阶!在一些传统椭偏仪中,使用“概览相机”或“并行监控像机” 是看不到这些特征的。因此,在搜索特定表面特征时,这些相机不得不依赖耗时的区域扫描。
获得专 利的感兴趣区域概念(ROI 概念)允许将测量和数据分析集中在视野内的选定特征上。
空间分辨率与探测光斑尺寸无关。因此,不需要严格的光束聚焦。
成像椭偏仪是什么样子的?
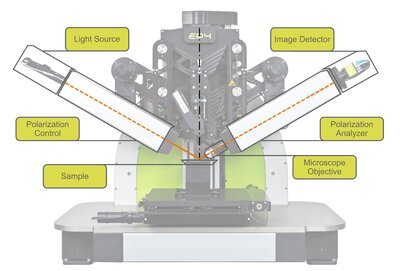 图 1:成像椭偏仪的特征组件
图 1:成像椭偏仪的特征组件基本几何形状类似于任何椭偏仪的典型设置:光源和偏振控制器安装在仪器的一个“臂”上,提供以倾斜入射角 (AOI) 照射样品的光束。探测光束从样品反射或透过样品,并由另一个“臂”收集以进行偏振分析和强度检测。 两个“臂”都安装在机械高精度测角仪上,以在不同的 AOI 处探测样品。
成像椭偏仪的显著特点是在检测“臂”中使用成像组件(图 1)。位于样品和偏振分析仪之间的显微镜物镜在数字图像检测器(CMOS相机的CCD)上创建被照明的样品表面的放大图像。该相机不仅用于监控探测的样品点(就像在常规椭圆偏振仪中那样),而且相机像素本身就是用于椭圆偏振测量的光电探测器。
成像椭偏仪如何测量椭偏光谱?
成像椭偏仪按顺序测量椭偏光谱。这意味着一次仅使用一种波长/光子能量。对光谱的每个目标波长自动重复测量。
我们的光谱成像椭偏仪配备宽带光源,例如激光稳定氙灯、氙弧灯或超连续谱激光器,并结合光栅单色仪、滤色轮或声光可调谐滤波器 (AOTF)。
成像椭偏仪是如何工作的?
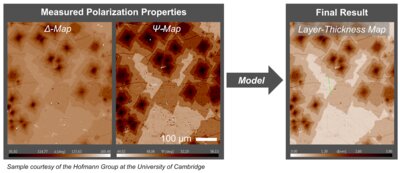 图 1:CVD 生长的石墨烯岛 - 测量的椭偏显微照片(Δ-Ψ-图,左)和 石墨烯层厚度图(右)从基于模型的 Δ 和 Ψ 像素级平移获得。
图 1:CVD 生长的石墨烯岛 - 测量的椭偏显微照片(Δ-Ψ-图,左)和 石墨烯层厚度图(右)从基于模型的 Δ 和 Ψ 像素级平移获得。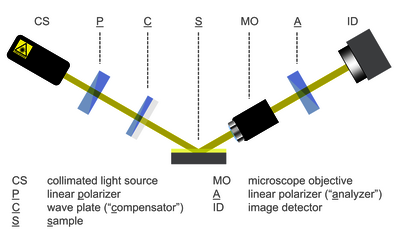 图 2:PCSA 配置中成像椭偏仪的示意图设置。
图 2:PCSA 配置中成像椭偏仪的示意图设置。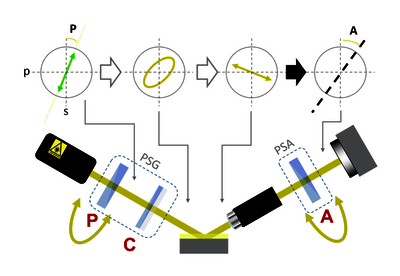 图 3:归零椭圆偏振原理。
图 3:归零椭圆偏振原理。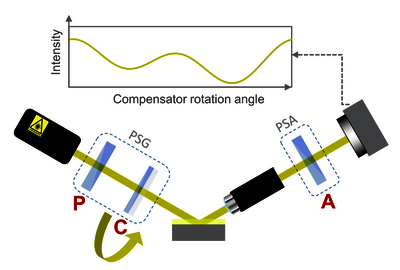 图4:旋转补偿器椭偏仪原理。
图4:旋转补偿器椭偏仪原理。成像椭偏仪延续了传统椭偏仪的测量原理:它们测量样品引起了探测光束偏振的变化。这种变化被转化为每个探测光子能量的两个实数,即所谓的椭圆参数 Δ (“Delta”)和Ψ(“Psi”)。 通过计算样品建模,这些参数转化为感兴趣的样品属性,例如:一层或多层的厚度、折射率和/或吸收率。
然而,与传统的椭偏仪相比,成像椭偏仪在调制探测偏振态和/或偏振分析仪(偏振调制)时采集显微镜图像堆栈(而不是“仅”强度值)。相机的每个像素都充当单独的光电探测器,从而并行测量超过 500 000 条强度曲线。然后显微镜图像的每个像素返回一个测量值Δ 和 Ψ,从而形成了所谓的 Δ-Ψ-图。因此,计算模型现在提供了像素级的转换 Δ-Ψ-图模型拟合结果的空间分辨显微照片,特别是厚度图和/或折射率图(图。1)。
Accurion 的成像椭偏仪应用所谓的PCSA(偏振器、补偿器、样品、分析器):偏振控制(或偏振状态发生器,PSG)包括线性偏振器和用于相位延迟的波片(“补偿器”)。偏振分析器(或偏振态分析器,PSA)位于显微镜物镜和图像检测器之间,仅包含一个线性偏振器(图2)。
三个偏振组件(P、C、A)安装在电动空心轴旋转器上,用于偏振调制。 Accurion 的成像椭偏仪采用以下方法: 归零椭偏仪和旋转补偿器椭偏仪。在这两种情况下,采集的图像堆栈的每个像素都会产生一条强度曲线,该曲线是所应用的 P、C 和 A 旋转角度设置的函数:
归零椭偏仪 (NE):归零模式迭代地旋转偏振器 (P) 和检偏器 (A) 以检测相对强度最小值的角位置,以便计算 Δ 和 Ψ(图3)。 这是各种椭圆偏振模式中高度 精 准的,对于检测折射率和/或层厚度的微小变化(例如单原子或单分子层阶)特别有用。
旋转补偿器椭偏仪 (RCE):RCE 测量相机信号作为补偿器旋转角度的函数(图 4)。它是市场上常见的椭圆偏振模式之一,因为它可以对所有类型的样品进行快速测量。
成像椭偏仪的一个突出特点是在单个仪器中提供这些互补的椭偏仪模式。
什么是光谱成像椭偏仪?
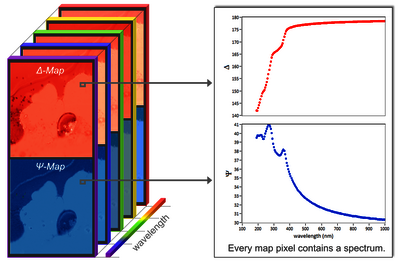 图 1:光谱成像椭偏仪获取的高光谱图堆栈的图示。
图 1:光谱成像椭偏仪获取的高光谱图堆栈的图示。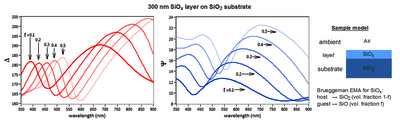 图 2:椭圆光谱示例显示对表面层轻微变化的敏感性增加。
图 2:椭圆光谱示例显示对表面层轻微变化的敏感性增加。光谱成像椭偏仪测量样品的椭偏特性作为探测波长(或光子能量)的函数。它产生高光谱 Δ-Ψ-图,其中每个图像像素都包含测量的椭圆光谱(图 1)。光谱测量是实现薄膜样品完整且高精度表征的通用方法(图 2)。因此,它们在过去二十年中已成为成像椭偏仪的标准用例。我们的大多数成像椭偏仪都配备了光谱测量功能。
得益于数码相机技术的进步和宽带光学组件的定制设计,Accurion 提供适用于电磁波谱的紫外线 (UV)、可见光 (VIS) 和红外线 (IR) 部分各种光谱范围的光谱成像椭偏仪。用于宽带测量的高端成像椭偏仪可以配备多达三个不同的相机,以覆盖从紫外线到红外线的整个光谱范围。
成像椭偏仪的数据分析是如何进行的?
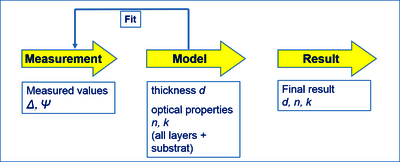 图 1:椭圆偏振测量和数据分析的流程图
图 1:椭圆偏振测量和数据分析的流程图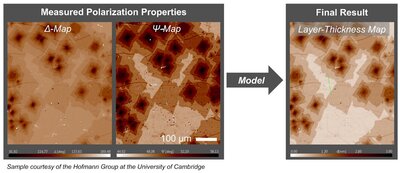 图 2:通过基于模型的 Δ 和 Ψ 像素级平移获得的 CVD 生长的多层石墨烯岛的测量椭偏显微照片(Δ-Ψ 图,左)和层厚图(右)。
图 2:通过基于模型的 Δ 和 Ψ 像素级平移获得的 CVD 生长的多层石墨烯岛的测量椭偏显微照片(Δ-Ψ 图,左)和层厚图(右)。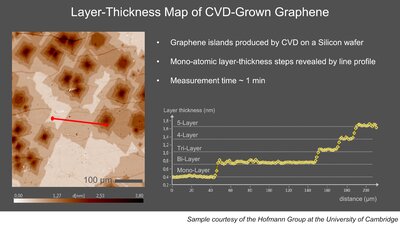 图3:成像椭偏仪的应用示例
图3:成像椭偏仪的应用示例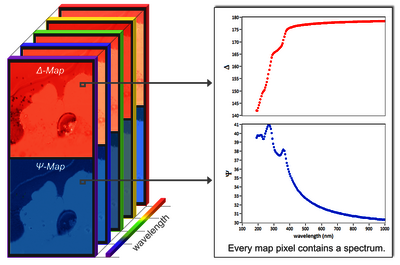 图 4:光谱成像椭偏仪获取的高光谱图堆栈的图示。
图 4:光谱成像椭偏仪获取的高光谱图堆栈的图示。成像椭偏技术本质上与常规椭偏技术有着相同的数据分析程序。测量得到的 Δ-Ψ-图主要用作传输量,从中计算出感兴趣的物理样品属性,例如层厚度、折射率和/或吸收率。 一般来说,这些值是从计算样本建模中获得的,其中包含未知样本属性作为浮动参数,并将模型与测量数据进行比较。通过回归分析,模型得出自由参数的最 终值,从而产生计算模型和测量数据的优质匹配(图1)。
此外,(高光谱)Δ-Ψ-图 还携带样品表面的结构信息(毕竟,它们是显微镜图像!),这些信息将被非成像测量忽略。这允许将椭偏数据分析与显微镜和高光谱成像的图像分析工
整个 Δ-Ψ-图 可以转换成物理样品属性的图像,例如显示整个测量表面的层厚分布的图像(图 2)。
直方图、横截面和线轮廓等工具有助于识别结构不规则性、评估值分布并区分阶梯状和梯度表面特征(例如层厚阶梯和梯度;图 3)。
测量后可以提取任何像素组的光谱,例如分别分析成像样品表面不同部分的层厚度和材料特性(图4)。
图像本身可能会揭示意想不到的表面特性,例如残留的清洁污染物或损坏,可能会扭曲建模结果,例如在常规(非成像)椭偏仪中。
什么是椭偏测量法?
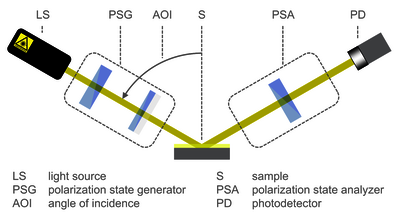 Figure 1: Schematic of an ellipsometer setup
Figure 1: Schematic of an ellipsometer setup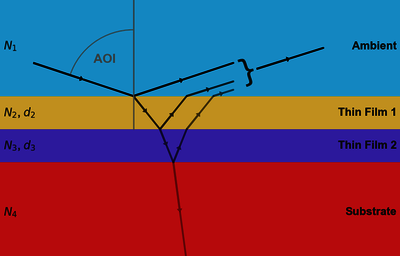 Figure 2: Superposition of reflected beams by a thin-film layer sample.
Figure 2: Superposition of reflected beams by a thin-film layer sample.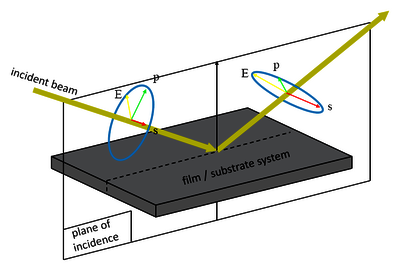 Figure 3: Orientations of the linear p- and s-polarizations in the coordinate system of an ellipsometer.
Figure 3: Orientations of the linear p- and s-polarizations in the coordinate system of an ellipsometer.椭圆偏振技术是一种非破坏性的表面表征光学技术。它通过以倾斜入射角 (AOI) 照射偏振电磁辐射(“光”)来探测样品。所施加的光子能量通常在电磁波谱的紫外线到红外线部分的范围内。椭圆偏振技术可检测并量化探测光束偏振椭圆的任何变化(因此称为“椭圆偏振技术”),这种变化可能在样品表面反射时发生(图 1)。
椭圆偏振测量对样品表面的任何变化都高度敏感。 特别是,椭圆光度法擅长表征平坦、反射样品表面上的透明或半透明薄膜涂层。厚度低于 1 nm 的薄膜层(即单原子层或单分子层)也可以作为厚度为几微米的层或层堆叠进行测量。
为了达到高标准的准确度和精密度,椭圆偏振测量法发挥了什么技巧?它归结为两个关键要素:
干涉透明或半透明薄膜层内多次反射引起的现象导致反射电磁波的幅度和相位对薄膜层厚度及其折射率的依赖性非常强(图2)。
探测样品偏振光和在倾斜兴趣区可以获取不同入射偏振状态的(相对)相位变化。该信息在垂直入射或缺乏偏振控制时会丢失(图 3)。
虽然反射测量等其他光学计量技术仅使用反射光束的强度(即反射波的振幅)来进行薄膜表征,但椭圆光度测量还可以获取样品引起的探测波的(相对)相移。这种额外的相灵敏度最 终为薄膜层表征带来了出色的精度和灵敏度。
椭圆测量将样品的偏振特性转化为每个探测光子能量的两个实数,即我们说的椭圆测量参数 Δ(“Delta”,相位信息)和 Ψ(“Psi”,幅度信息)。
为了理解这些量的详细含义,我们需要引入样品表面偏振电磁(EM)波镜面反射的数学描述。一般来说,入射电磁波的振幅和相位会因反射而改变。然而,在倾斜 AOI 中,p 偏振波和 s 偏振波的这些变化量是不同的(图 3),因此我们可以写为:

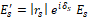
E'p 和 E's是复数(i 虚数单位),分别表示样品表面反射之前和之后p偏振和s偏振电磁波的电场幅度和相位;rp,s 和 δp,s 分别是样品引起的幅度和相位变化。
最 后,我们可以给出椭偏参数的数学定义 Δ 和 Ψ :

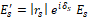
因此,Δ 是 p 偏振和 s 偏振电磁波的样品引起的相位差,而 Ψ 量化样品引起的这些波的振幅变化的比率。
椭偏测量法是如何工作的?
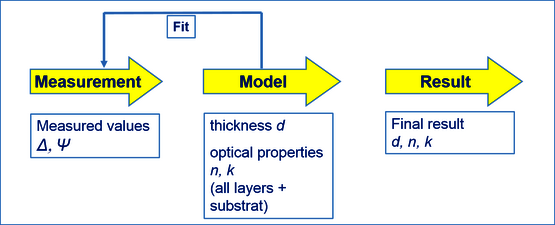 图 1:椭圆偏振测量和数据分析的流程图
图 1:椭圆偏振测量和数据分析的流程图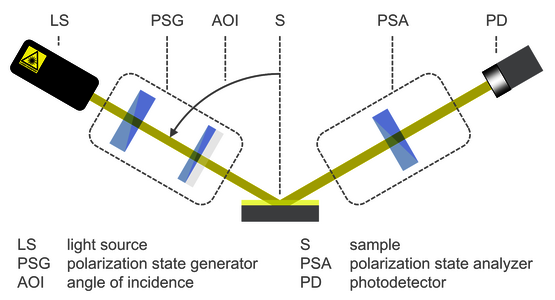 图 2:椭圆偏振仪的基本设置
图 2:椭圆偏振仪的基本设置任何椭偏样品表征至少包括两个步骤:
第 一步,椭圆偏振仪测量样品引起的偏振变化,每个探测光子能量可以将其转化为两个实数。 这些就是所谓的椭偏参数 Δ(“Delta”)和 Ψ(“Psi”)。 这些参数可以理解为所研究的样品如何与偏振光相互作用的“指纹”。
第二步,测量值 Δ 和 Ψ 用于计算感兴趣的样品属性,例如层厚度、折射率和/或吸收率。 专门的数据分析软件使用样本的计算模型来计算预期值 Δ 和 Ψ 并将其与测量值进行比较。 然后将感兴趣的属性用作浮动参数,以找到实验数据和模型数据的优质匹配。因此,椭圆光度术是一种基于模型的(间接)光学厚度和折射率测量技术。
为了执行椭偏测量,任何椭偏仪设置至少由四个组件组成:光源、偏振态发生器 (PSG)(由一些偏振光学器件组成并放置在样品之前)、偏振态分析仪 (PSA); 更多偏振光学器件)放置在样品后面的光束路径中,以及光电探测器。 PSG 和 PSA 分别控制和分析探测光和反射光的偏振态。
Δ-和Ψ-值的测量基于针对偏振控制和/或偏振分析(偏振调制)的不同设置的一系列强度测量。根据这些强度值以及 PSG 和 PSA 的已知设置,可以直接计算 Δ- 和 Ψ- 值。
PSG 和 PSA 设计有多种类型,应用的偏振调制模式甚至更多。 Accurion 的椭偏仪采用非常常见的设计,即使用线性偏振器和四分之一波片(λ/4 板)作为 PSG,以及使用单一线性偏振器作为 PSA。对于偏振调制,他们应用了以下技术归零椭偏仪和旋转补偿器椭偏仪。
























