作者:郭睿
一 问题的提出
重叠峰的剥离是电子探针分析的难点之一。例如,TiN 作为涂层材料经常被要求给出准确的定量分析数据。
N Kα 和 Ti Ll 线系相差仅 3eV(N Ka=0.392keV;Ti Ll=0.395keV),即使当前Z高 级别的电子探针波谱仪也无法将二者分开。忽略 Ti Ll 线系对 N Kα 线的“贡献”会造成定量分析结果的严重偏差。
日本电子的探针提供一个标准软件(Interference Correction),可以很好的解决这一问题。
二 解决办法的物理背景
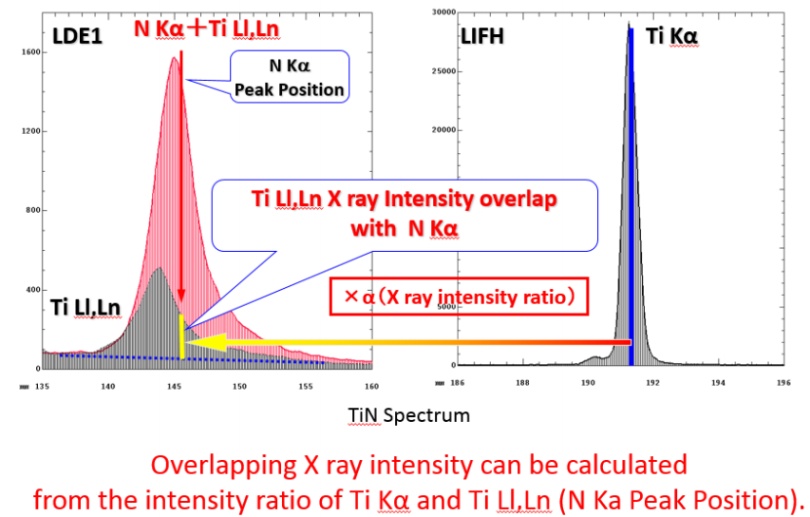
上图是待测样品 TiN 的电子探针分析图。右上图为 LIH 晶体测得的 Ti 的主线系 Ti Kα, 左上图为使用 LDE1 晶体测得的 N Kα 谱图(红色为 N 的谱图,黑色为 Ti 的次级线系Ti Ll 和 Ti Ln 的谱图,以下简称为 Ti Ll 谱图)。左上图中黄色线段是 Ti 的“贡献”,是需要扣除的,我们称之为“干扰峰强度”,红色线段是我们所需要的 N 的真实峰值,我们称之为“待测元素实际强度”。
Interference Correction 方法的关键点就是准确测量校正系数 α,α=标准样品 Ti Ll 强度值/标准样品 Ti Kα 标准样品强度值,如下图所示:
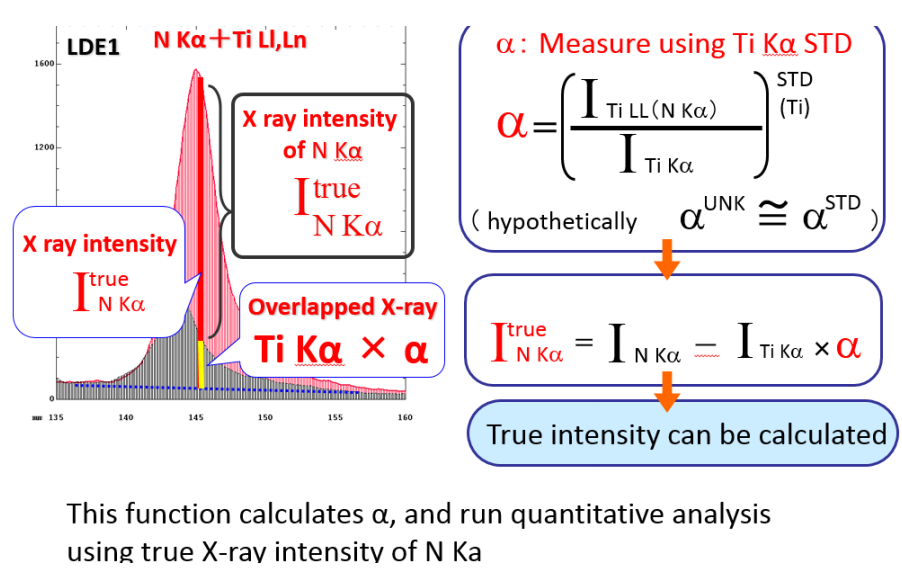
干扰峰 Ti Ll 的强度值=α*待测样品 Ti Kα 的实际强度值
待测元素 N Kα 的强度值(净值)=N Kα 峰值处实测强度值 - 干扰峰 Ti Ll 的强度值
操作步骤如下:
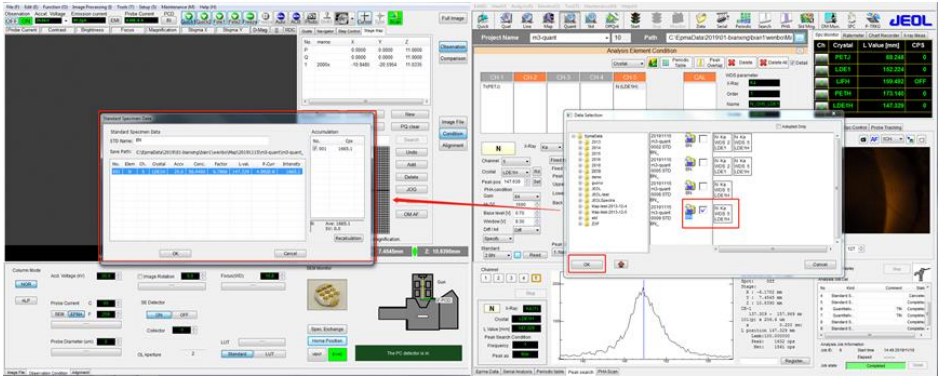
⚫ 选择区别于待测样品 TiN 的含 N 标准样品,例如 BN,准确测量 N 的峰值和左、右
背景值
⚫ 选择区别于待测样品 TiN 的含 Ti 标准样品,例如纯 Ti,准确测量 Ti 的 Ti Kα 峰值以及在 N 元素峰值处的 Ti Ll 强度值(注意不是 Ti Ll 的峰值),以便获得准确的干扰系数 α ⚫ 实测待测样品 TiN 中的 Ti Kα 的强度值以及 N 元素 Kα 峰值处的强度值,程序会自动获得 N 元素 Kα 的净值
三 具体实验步骤
1.标准样品的录入和标样的测量
⚫ 将 Ti 的标准样品纯 Ti 和 N 的标准样品 BN,以及 TiN 样品装入探针内
⚫ 录入 Ti 的标样和 N 的标样信息,注意:准确找到标准样品位置,将十字叉丝调节清晰,录入标准样品的名称,成份信息,以及位置信息
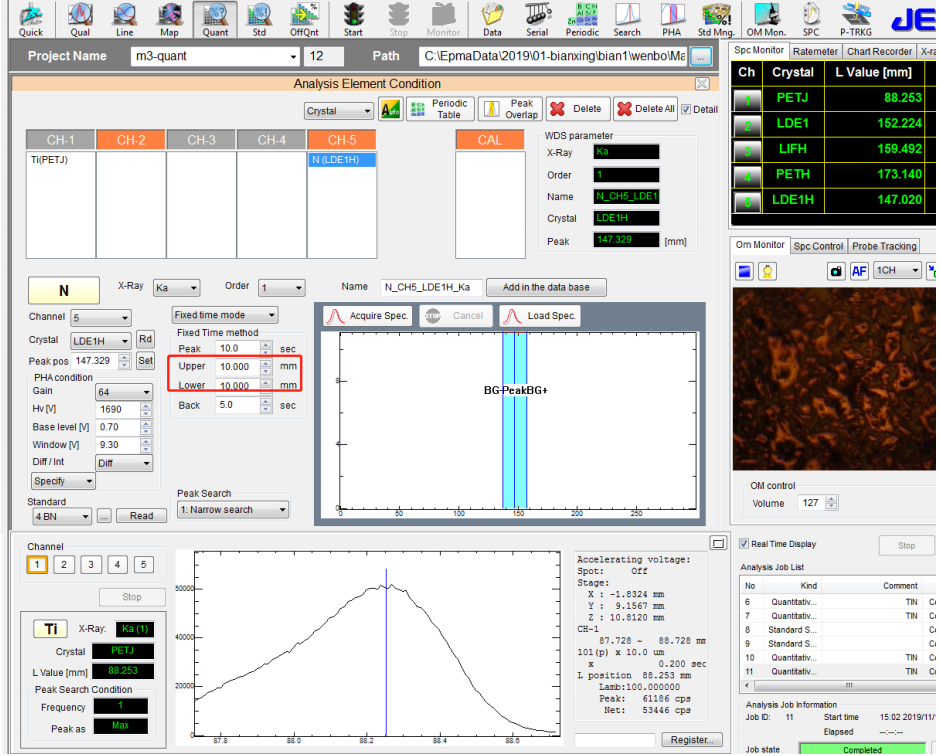
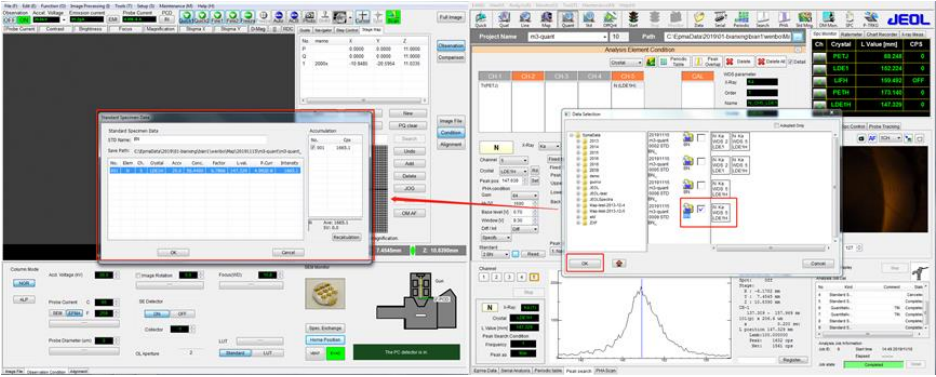
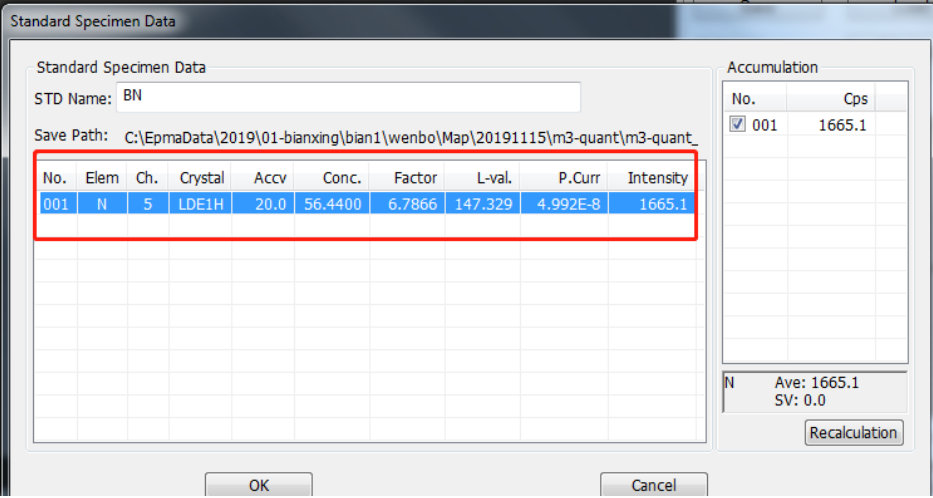
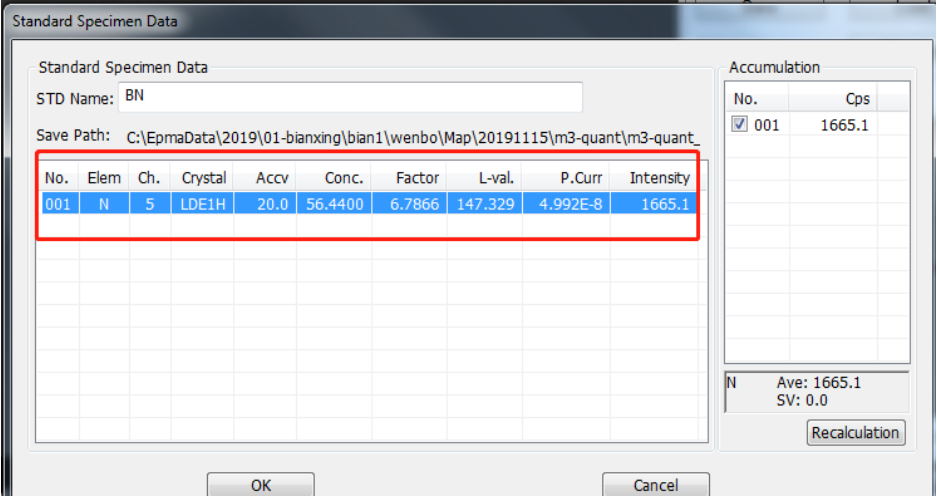
⚫ 将 N 标样 BN 进行标样检测,电子光学条件是 20kV,50nA,如下图所示:
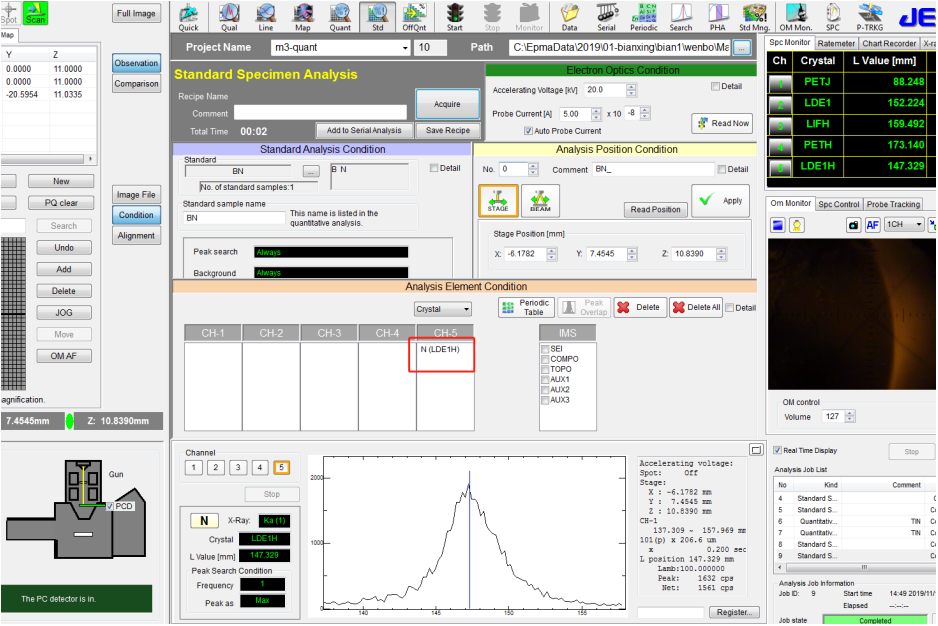
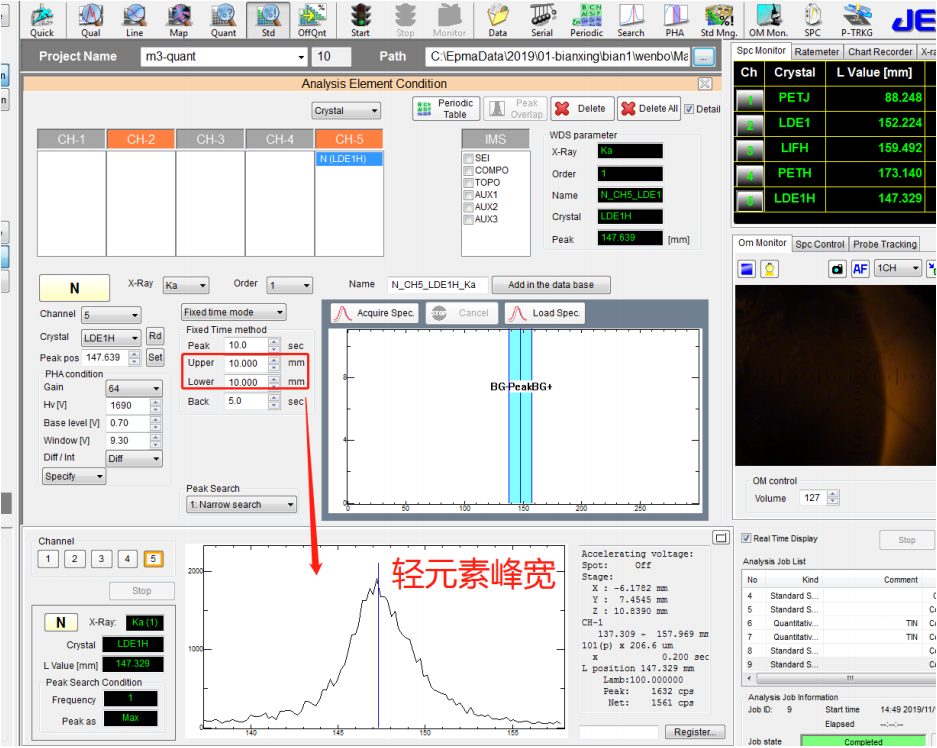
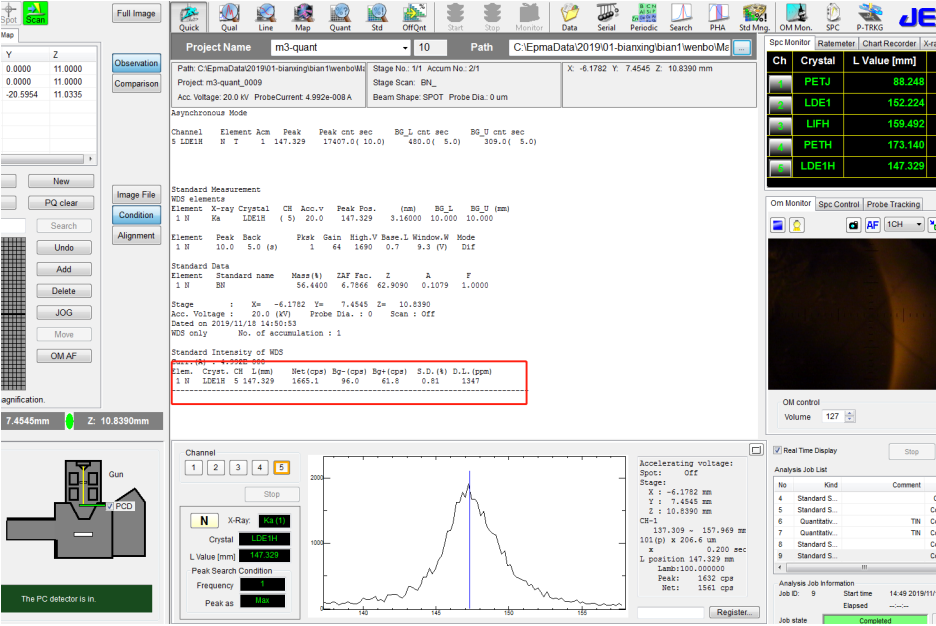
⚫ 将 Ti 的标样进行标样检测,电子光学条件同上,如下图所示:
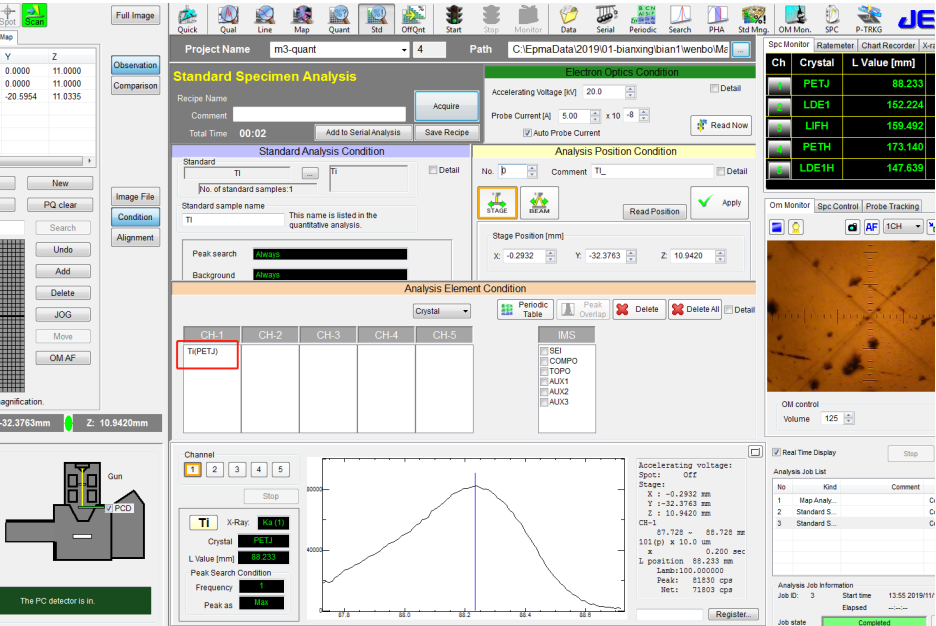
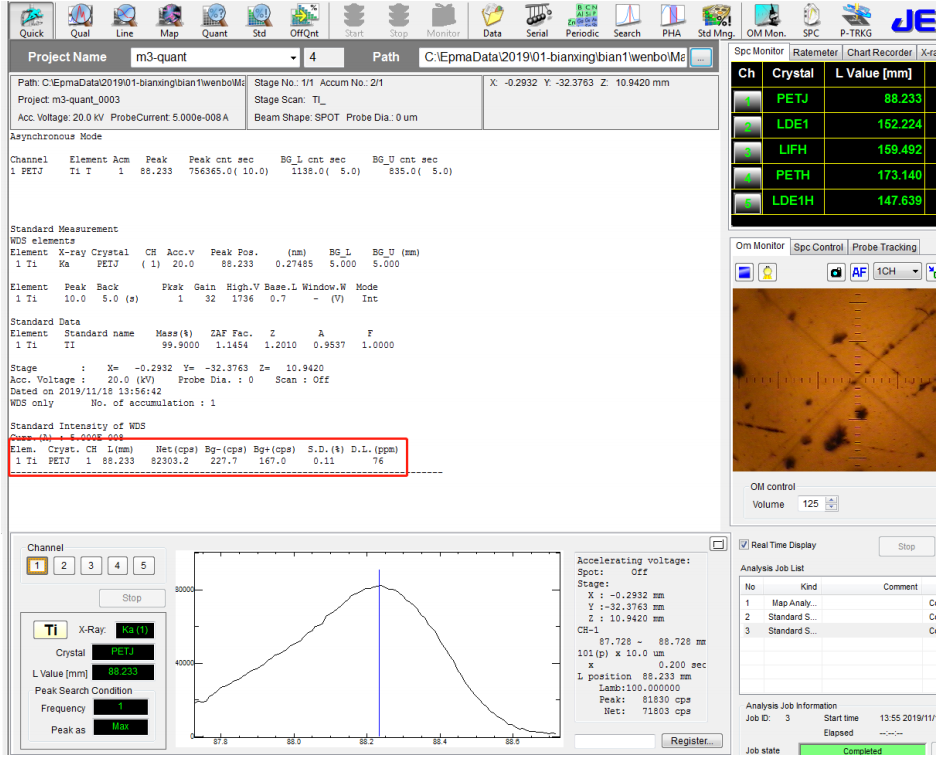
2. 常规方法进行未知样品 TiN 的定量分析(不使用 Interference Correction 校正)
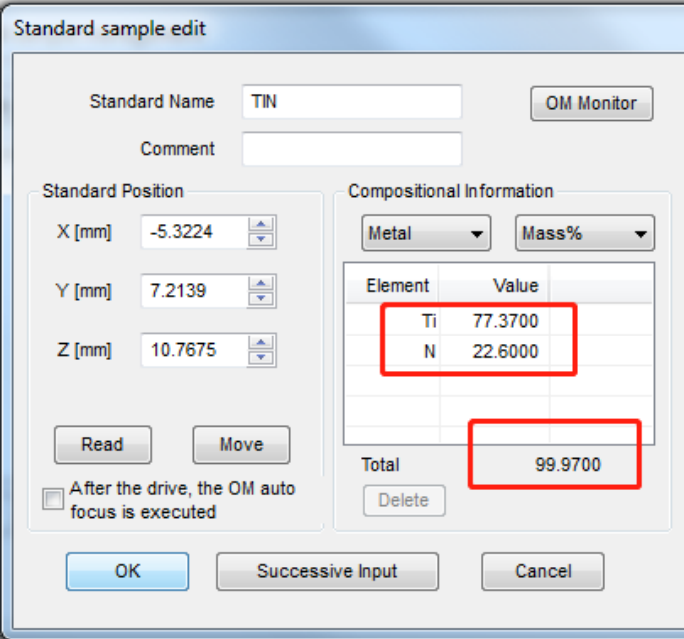
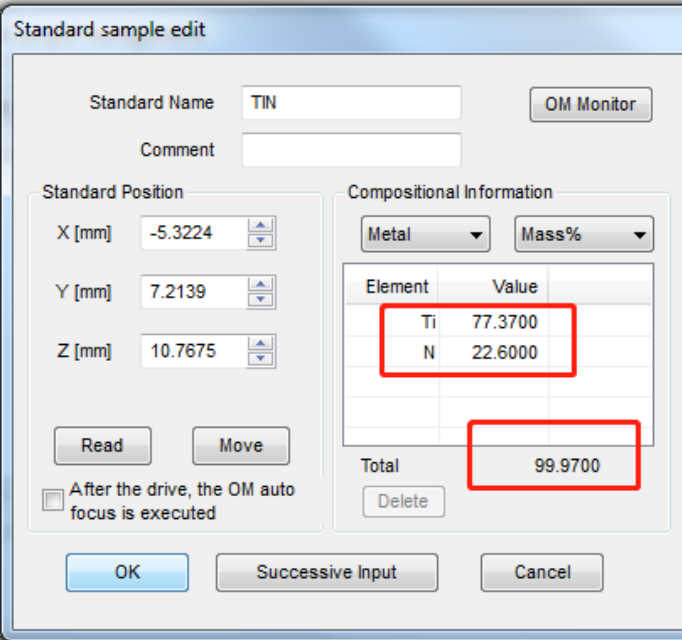
⚫ “未知样品”选择的是国产标样 TiN(Ti:77.37%;N: 27.6%;纯度 99.97%)
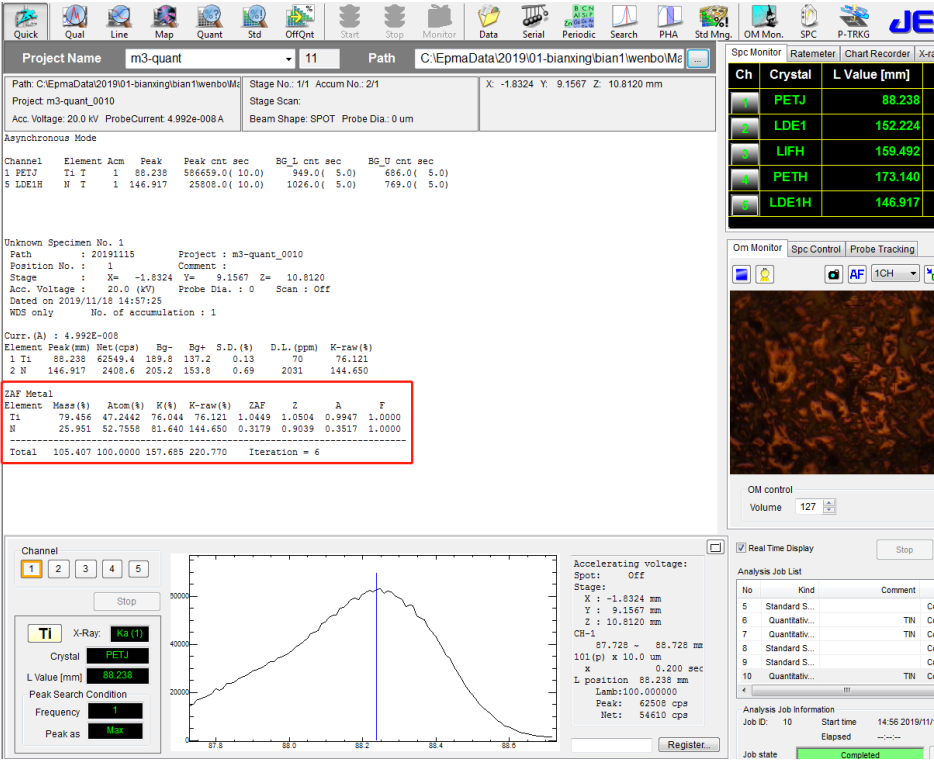
⚫ 对上述 TiN 样品进行常规定量分析,电子光学条件 20kV,50nA,Ti 选择的是 PETJ
晶体,N 选择的是 LDE1H,并采用的 Metal-ZAF 定量分析方法,如下图所示:
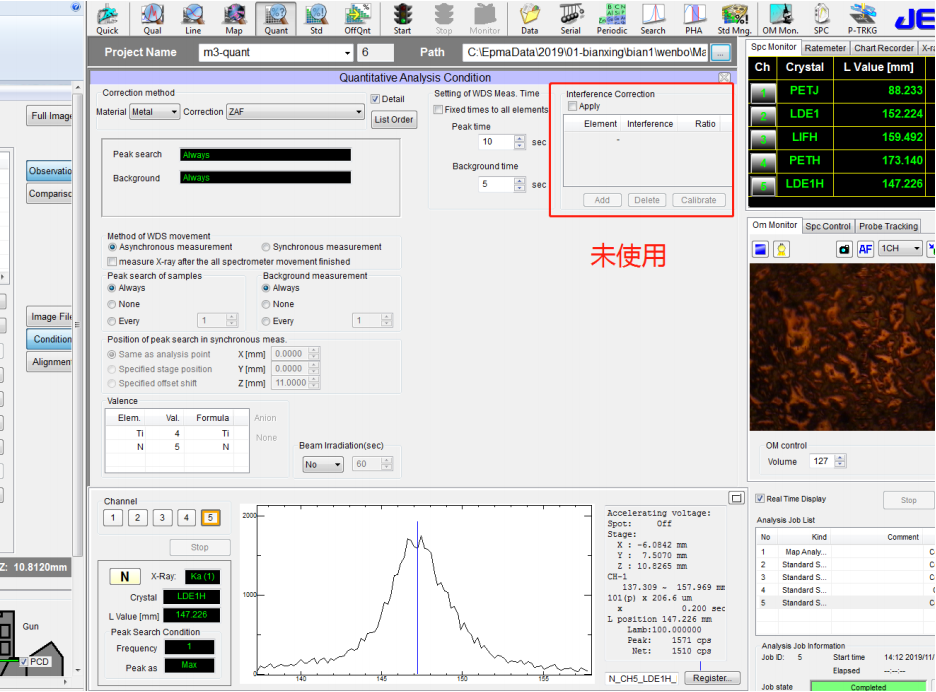
⚫ 注意上述红框中未“勾选”,这意味着定量分析未进行重叠峰校正
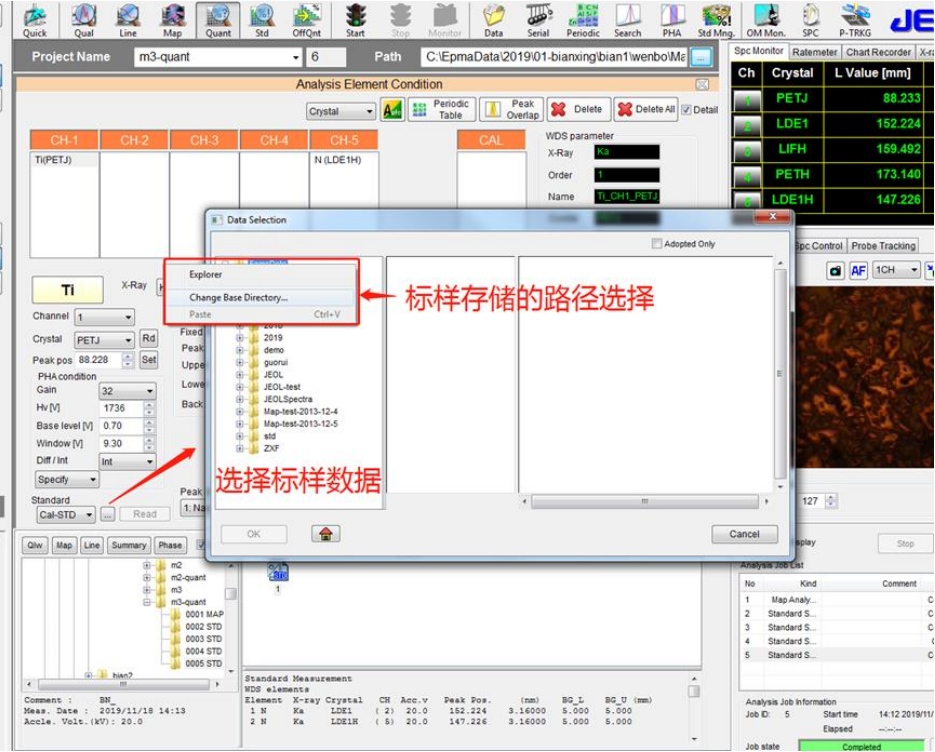
⚫ 鼠标单击 Data-Selection 对话框中的文件夹,可以进行标样的存储路径选择,选择合适的标样
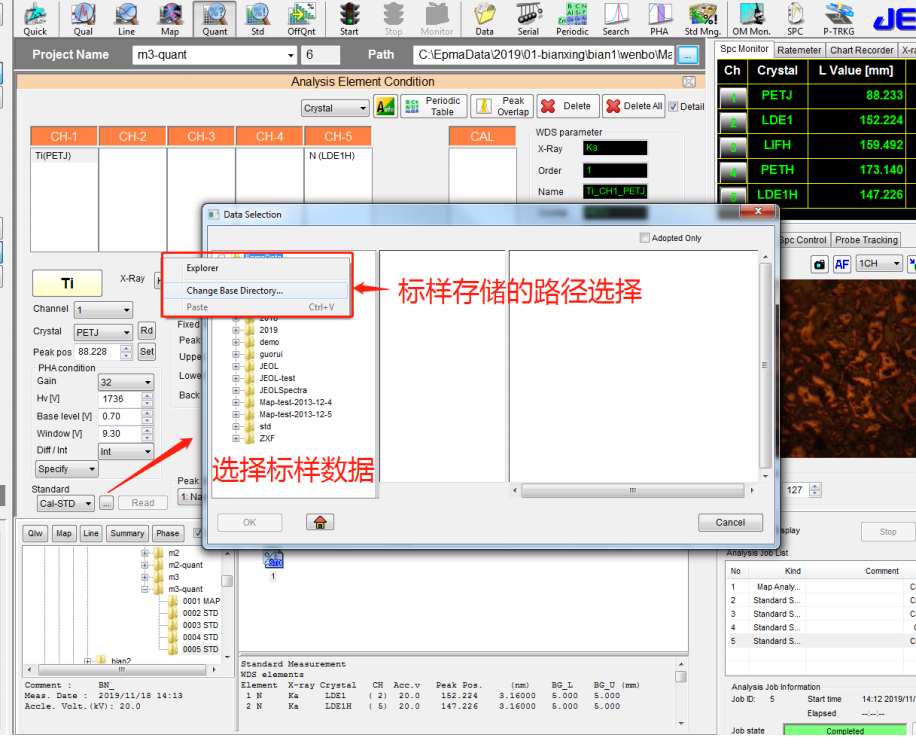
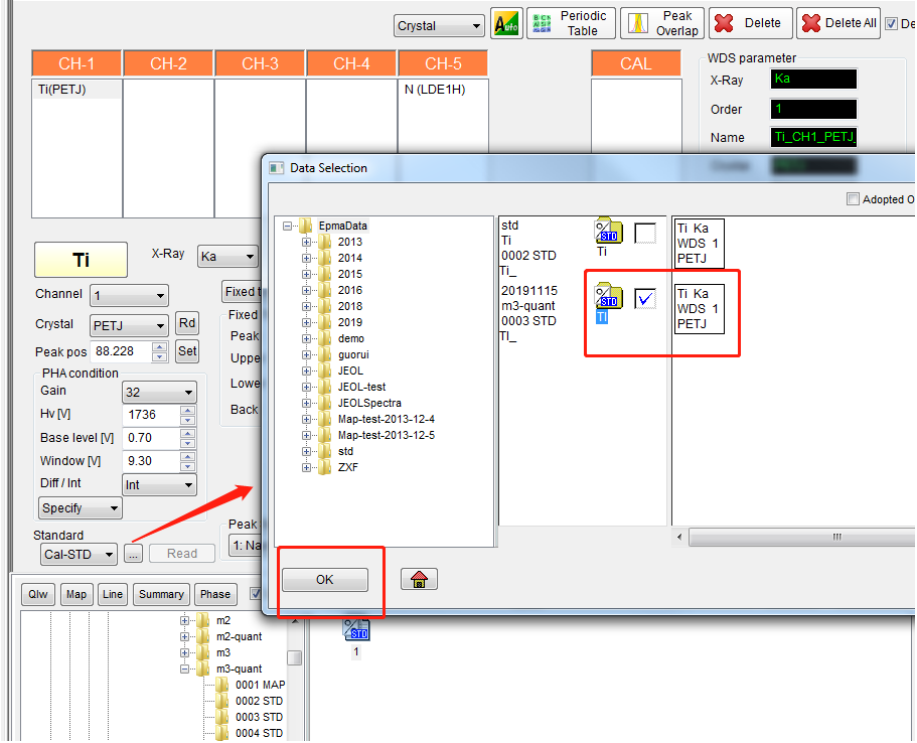
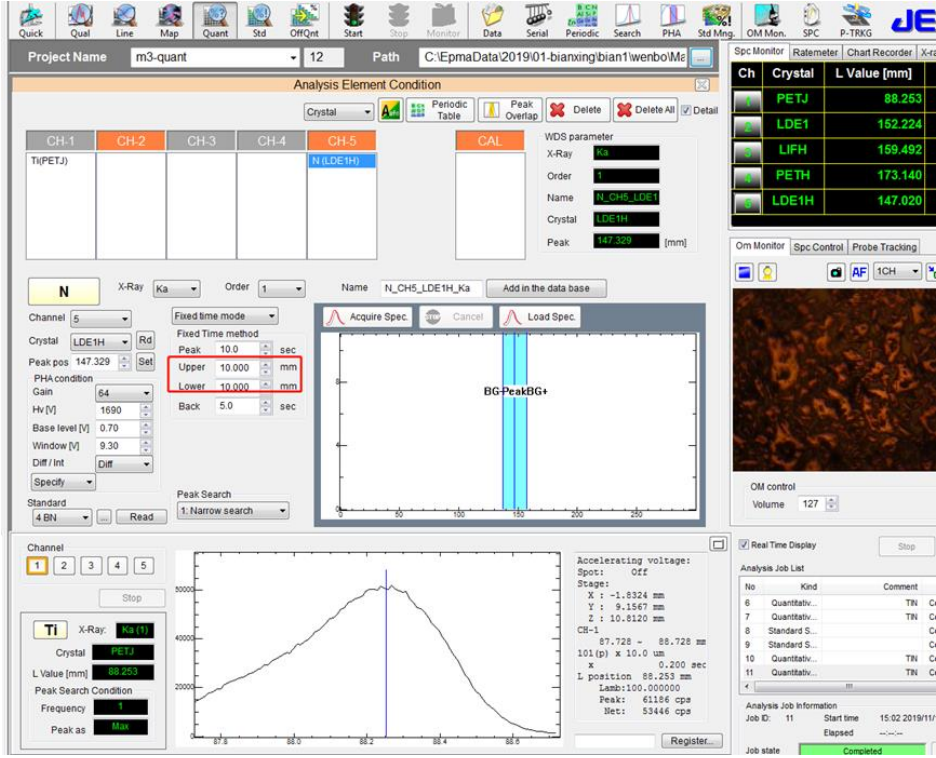
⚫ N 元素的左、右背景值分别选择 10mm,选择好 N 的标准样品数据
⚫ 执行定量分析后,得到如下图的结果。与国产标样 TiN 的真实含量进行比对,发现定量数据偏差较大,而且总量偏差也较大
标样数值:Ti:77.37%;N: 22.6%;纯度 99.97%
未经重叠峰校正的定量分析数值:Ti:79.46%;N: 25.96%;总量 105.4%
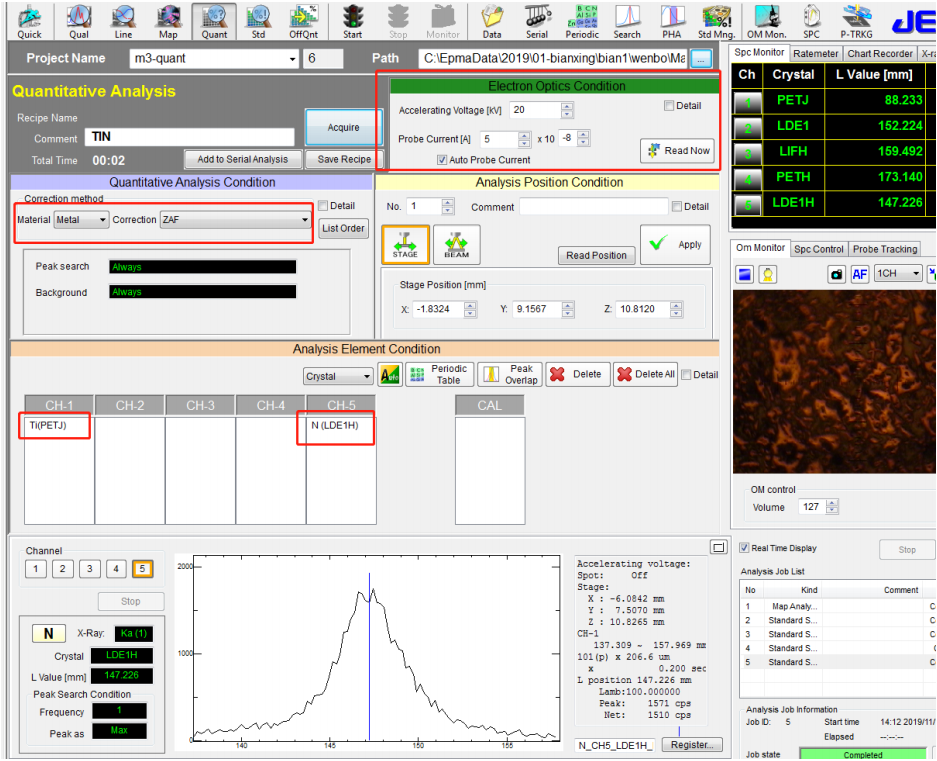
3. 使用 Interference Correction 校正进行未知样品 TiN 的定量分析
⚫ 将 TiN 作为待测样品进行检测,电子光学条件 20kV,50nA,Ti 选择的是 PETJ,N 选择的是 LDE1H,采用的是 Metal-ZAF 定量分析条件,
如下图所示:
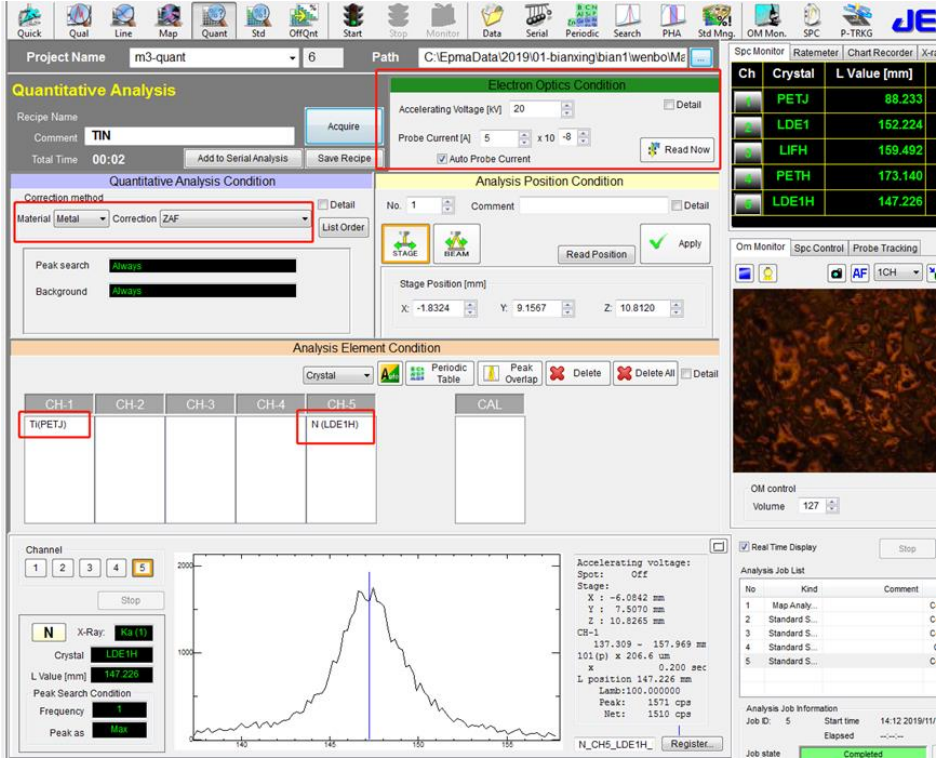
⚫ 鼠标单击 Data-Selection 对话框中的文件夹,可以进行标样的存储路径选择,选择合适的标样
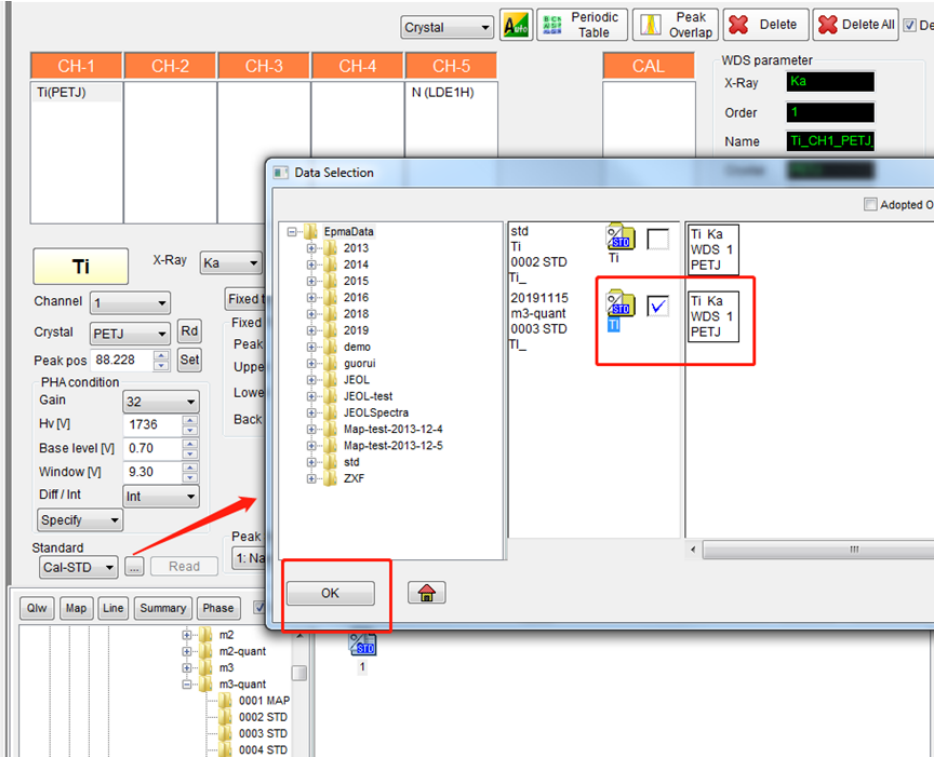
⚫ N 元素的左、右背景值选择 10mm,选择好 N 的标准样品数据
⚫ 在 Quantitative analysis condition 中,在 Interference Correction下面的 Apply 前的复选框打钩。在 Element 下选择 N 以及通道和分光晶体,注意,这里选择的是被干扰元素。这与 Analysis Element Condition中选择 N 的通道和分光晶体对应。在 Interference 下面选择 Ti 以及通道和分光晶体,注意,这里选择的是干扰元素。这与 Analysis ElementCondition 中选择 Ti 的通道和分光晶体对应。
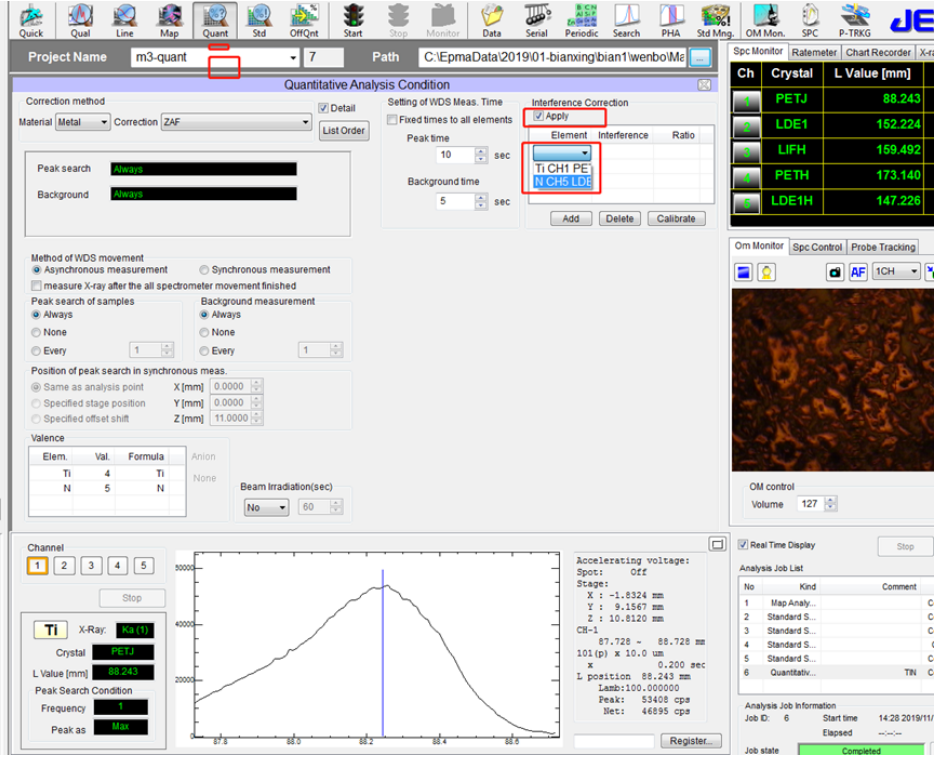
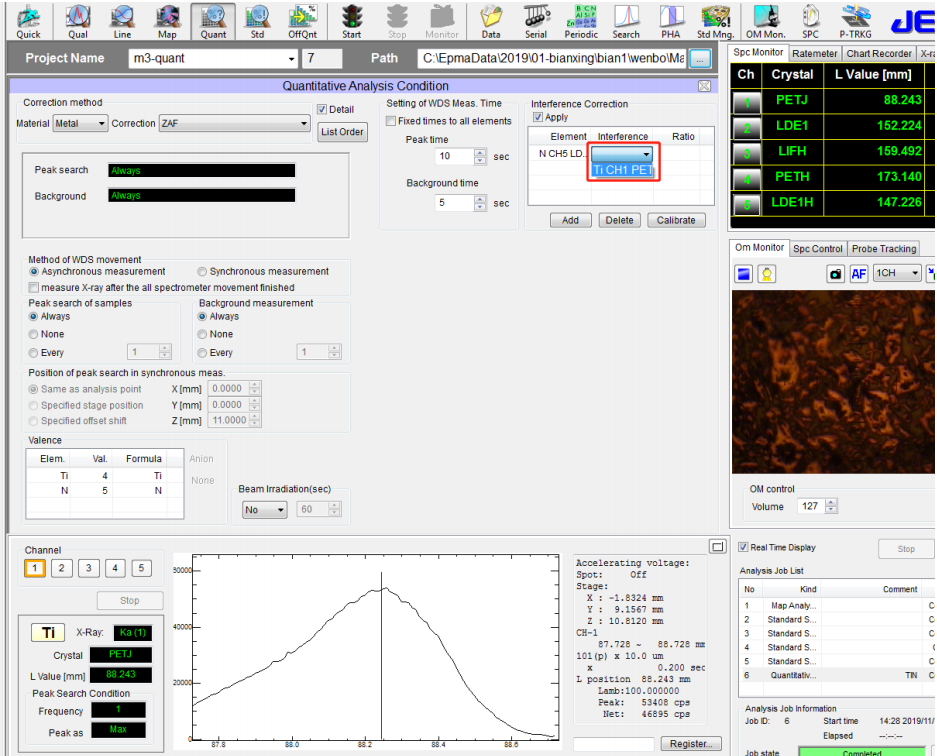
⚫ 点击 Calibrate,目的是要计算 Ratio,会有对话框弹出,再确认 Ti 的标准样品(纯 Ti)以及 N 的标准样品(BN)的坐标位置,以及十字叉丝调节清晰,确认无误后,点击 Start。

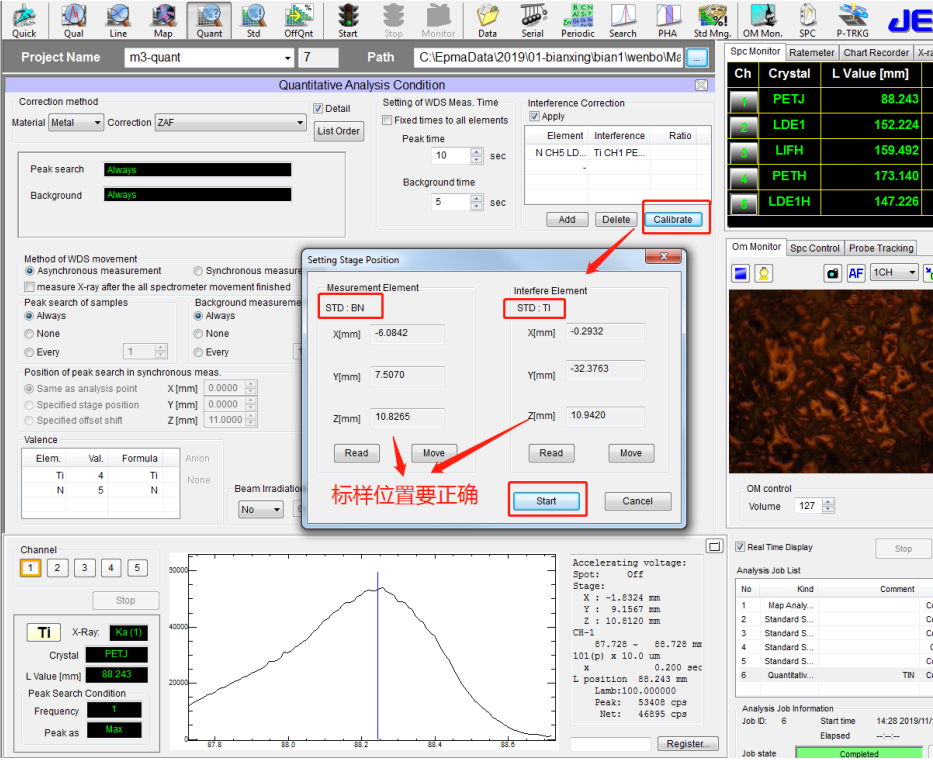
⚫ Ratio 下面显示开始运行“Running”
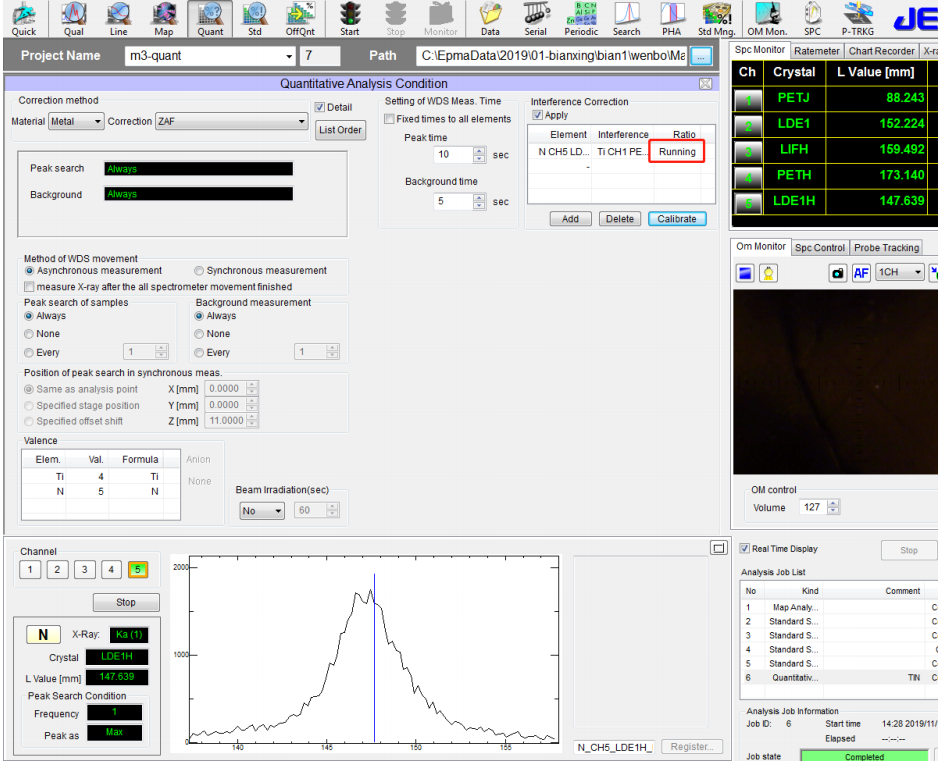
⚫ 程序运行完成后,Radio 得到值 0.0100(程序运算值),并自动显示
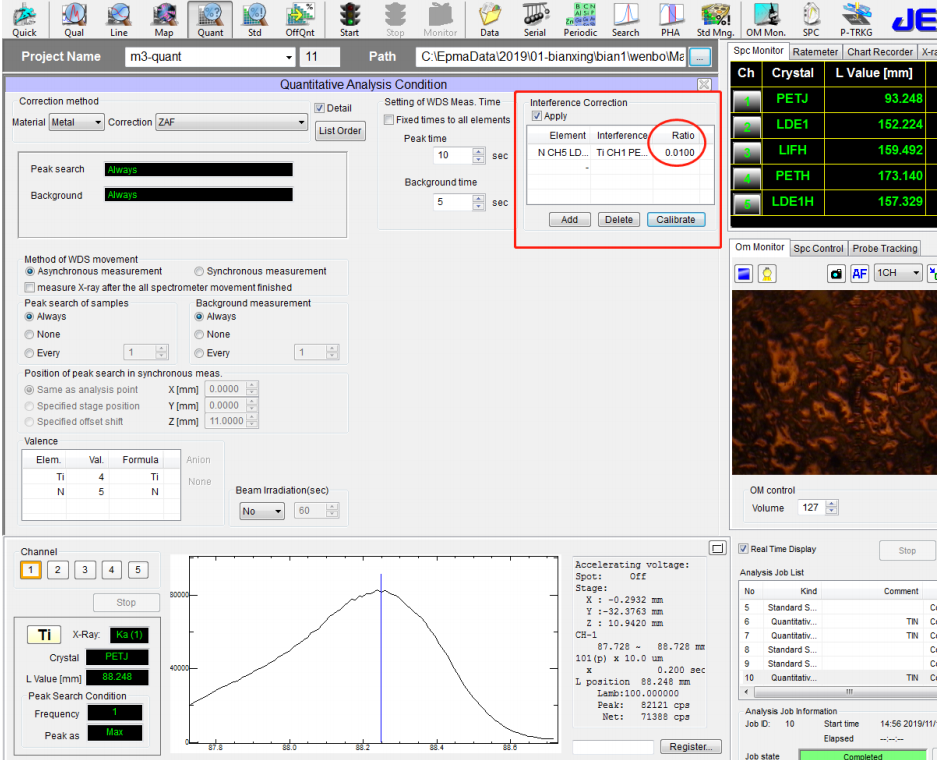
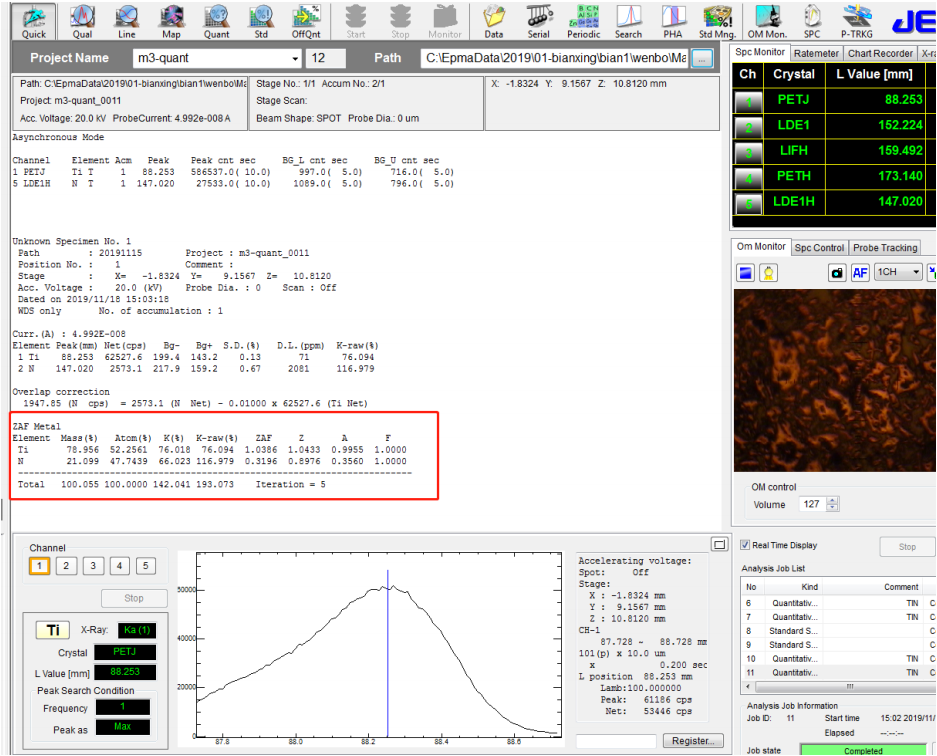
⚫ 执行定量分析后,得到如下图的结果,与 TiN 的真实含量以及未经校正得到的定量数据比对,发现经过重叠峰校正后的数据明显、大幅改善,说明该种校正非常有效。
标样数值:Ti:77.37%;N: 22.6%;纯度 99.97%
经重叠峰校正的定量分析数值:Ti:78.96%;N: 21.09%;总量 100.05%
四 总结
⚫ Interference Correction 可以有效地解决电子探针中重叠峰的问题,对重叠峰有效地剥离,正确的计算出两个重叠元素各自真实的含量。
⚫ 电子探针中还有其它重叠峰剥离方法,例如 Spectrum De-convolution Analysis Program 程序,该程序是利用Z小二乘法进行重叠峰的剥离,属于选购软件,我们不建议推荐该软件。因为标准配Interference Correction 方法能够胜任大多数工作。
五 小知识
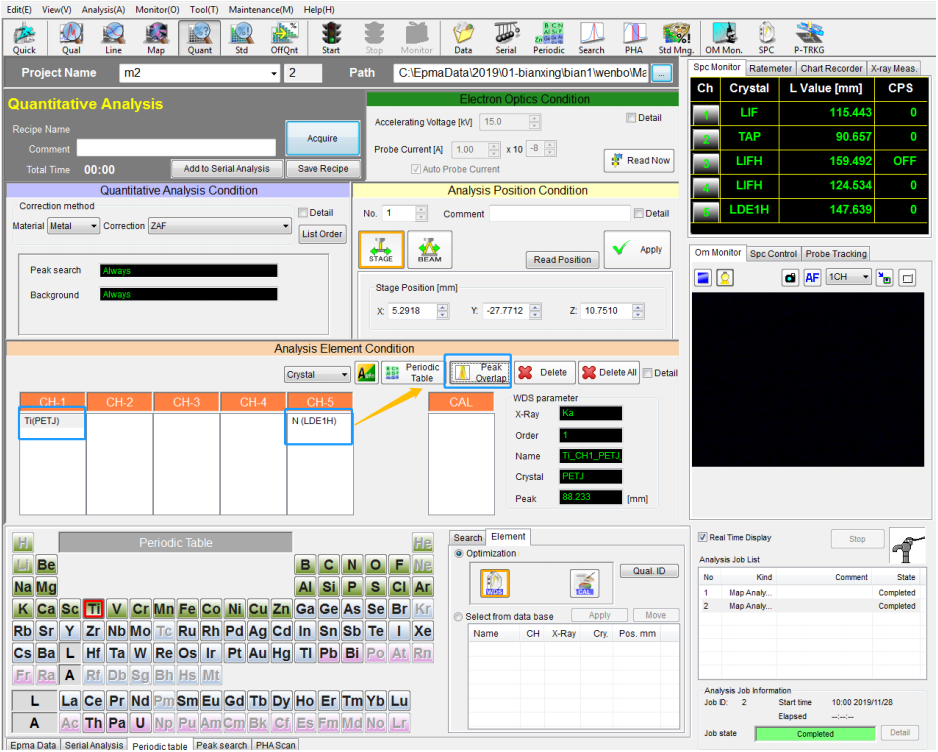
⚫ 如何判断出两个元素重叠与否呢?在 Analysis Element Condition 中,选择这两个元素,如下图所示,选择 Ti 与 N,点击 Peak Overlap
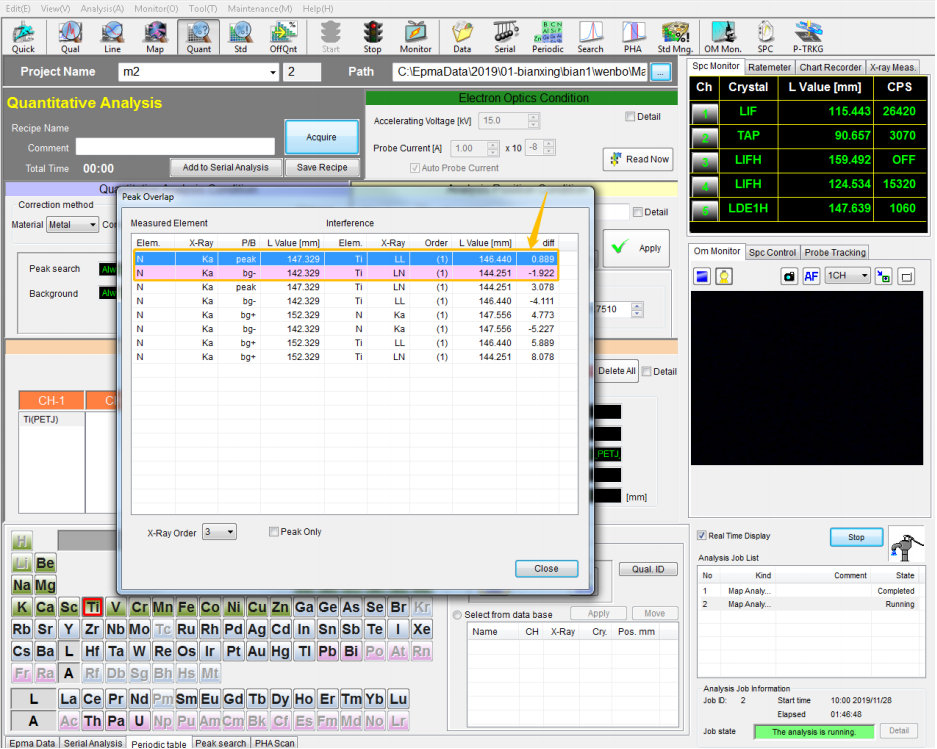
⚫ 如下图所示,蓝色区域:N Kα 线峰 peak 位置和 Ti Ll 一阶线非常相近,两条线的 L 值的“diff”距离是 0.889mm;N Kα 线下背底“bg-”位置和 Ti LN 一阶线非常相近,两条线的 L 值的“diff”距离是 1.922mm

 评论
评论