无限大均匀带电平面两侧的场强为 E=δ/2ε,这个公式对于靠近有限大小带电面的地方也适用,这就是说,根据这个结果,导体表面元ΔS 上的电荷在紧靠它的地方产生的场强也应是E=δ/2ε ,但是,我们知道,在静电平衡状态下,导体表面之处附近空间的场强E 与该处... 无限大均匀带电平面两侧的场强为 E=δ/2ε,这个公式对于靠近有限大小带电面的地方也适用,这就是说,根据这个结果,导体表面元ΔS 上的电荷在紧靠它的地方产生的场强也应是E=δ/2ε ,但是,我们知道,在静电平衡状态下,导体表面之处附近空间的场强E 与该处导体表面面电荷密度 δ的关系为E=δ/ε ,前者比后者小半,这是为什么?
若一带电导体表面上某点附近电荷面密度为δ 这时该点外侧附近场强为E=δ/ε ,
如果将另一带电体移近,该点场强是否改变?公式E=δ/ε 是否仍成立?
“……根据这个结果,导体表面元ΔS上的电荷在紧靠它的地方产生的场强也应是E=δ/2ε ”这个推理不对。平面两侧都有电场线(且对称),但导体表面的两侧却大不一样——内侧无电场线,外侧电场线要多一倍,这是高斯定律要求的——同样多的电荷,要有同样多的电通量。对于同样的扁圆柱形高斯面,无限大平面时上下两底面有同多的电场线穿过;导体表面时则只有一个底面有电场线穿过,它就必须使这里通过的电场线多一倍才能保证整个圆柱表面的电通量一样。
可以从点电荷的电场的叠加来理解,导体表面各处的电荷以及外电荷的各自的电场在导体内部要彼此大体上反向才能使内部的总场强为零,但各自的电场在导体的外部就大体同向而使总场强“加倍”。想想平板电容的两板带等量同种电荷时的情景,每板的电场在板的两侧都是δ/2ε,但两板的电场在两板之间的“内部”空间里是彼此反向的,使得总场强为零;两板各自的电场在两板以外的“外部”空间里则是彼此同向的,使得总场强加倍为δ/ε。
“若一带电导体表面上某点附近电荷面密度为δ,这时该点外侧附近场强为E=δ/ε,如果将另一带电体移近,该点场强是否改变?公式E=δ/ε是否仍成立?”——那里的电场改变了,公式E=δ/ε仍成立。正是别的带电体的出现使那里电荷面密度变化了,所以电场才改变。


 赛默飞半导体加速和高级服务组合,为您提供网络支持
赛默飞半导体加速和高级服务组合,为您提供网络支持
 半导体杂质检测难?半导体专用ICP-MS来帮你!
半导体杂质检测难?半导体专用ICP-MS来帮你!
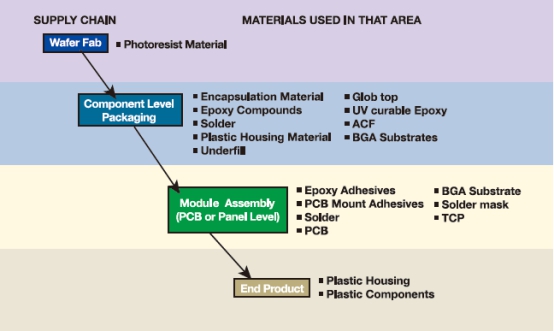 半导体封装行业的热分析应用
半导体封装行业的热分析应用
 户外条件下进行半导体芯片激光焊接:你确定?
户外条件下进行半导体芯片激光焊接:你确定?

 评论
评论