| 行业应用: | 农林牧渔 综合 |
背景
Sauerbrey 1 是*一个认识到石英晶体微天平(QCM)技术潜在用途的人,并证明了这些压电器件对 QCM 电极表面质量变化的极其敏感的性质。他的研究结果体现在 Sauerbrey 方程中,该方程将QCM 电极表面单位面积的质量变化与观察到的晶体振荡频率的变化联系起来:∆f = - Cf .∆m (equation 1)
其中,
∆f-观察到的频率变化,以 Hz 为单位,
∆m-单位面积质量变化,以 g/cm2 为单位,C f -所用晶体的灵敏度系数(即 56.6 Hz µg -1 cm2 用于室温下 5MHz AT-cut 石英晶体)。
Sauerbrey 方程依赖于线性灵敏度系数 C f ,这是 QCM 晶体的一个基本特性。因此,在理论上,QCM 质传感器不需要校准。然而,必须记住的是,Sauerbrey 方程只严格适用于均匀的、刚性的、薄膜沉积2 。真空和气相薄膜沉积不能满足这些条件,实际上表现出更复杂的频率-质量相关性,通常需要一些校准才能得到准确的结果。多年来,QCM 一直被认为是气相质量探测器;然而,*近,随着科学家们意识到它们可以与液体和粘弹性沉积物接触,使得它们的应用得到了扩展。在这种情况下,石英振荡器的频率和串联谐振电阻对于完*表征与晶体电极接触的材料是非常重要的。用于流体的 QCM 开发开辟了一个新的应用领域,包括电化学和微流变学。*近的发挥在那集中在定制电极表面化学(即专门的聚合物涂层),以便这些设备可以被应用于(1)特定气体检测,(2)环境监测,(3)生物传感,(4)基本表面分子相互作用研究的鉴别质量检测器。
本章的目的是为QCM用户提供不同的测量和校准技术的简要介绍,并简要描述用于解释结果的、*常用的理论模型。对这些主题的全面讨论显然超出了本说明的范围。然而,从真空薄膜沉积到电化学实验中,已经发表了许多关于 QCM 的操作和校准的文章,QCM 用户可以参考本章末尾的出版物列表以获得更详细的信息。
QCM 振荡器
石英晶体谐振器的 Butterworth van Dyke(BVD)电学模型3 如图 1 所示。该模型常用于表示晶体谐振器在接近串联谐振时的电学行为,该模型在预测 AT-cut 石英晶体在 QCM 应用中的频移和损耗方面也很有用。
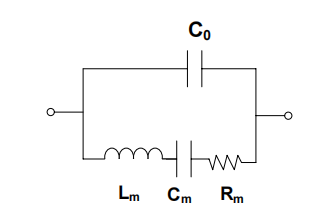
图 1:石英晶体谐振器的 Butterworth van Dyke 模型。
BVD 电模型由两条电路组成。运动臂具有三个系列组件,由晶体的质量和粘性载荷修改:(1)R m(电阻)对应于安装结构和与晶体接触的介质的振荡能量耗散(即粘性溶液引起的损耗),(2)C m(电容)对应于振荡中存储的能量,与石英和周围介质的弹性有关;(3)L m(电感)对应于振荡的惯性分量,它与振动过程中位移的质量有关。对于 QCM 系统中使用的直径 1 英寸的 5MHz 晶体,这些参数的典型值为 C m =33fF,L m =30mH 和 R m =10Ω(用于干晶体),R m =400Ω(水中的晶体),或 R m =3500Ω(88%甘油的晶体)。
运动臂由寄生电容 C o 分流,C o 表示晶体电极、支架和连接器电容的静态电容之和。在 QCM 系统4 中,C o 约为 20pF,通过将电子器件直接放置在晶体支架上,从而消除电缆电容,从而保持了较小的值。
在 QCM 应用中,当质量增加到晶体电极时,运动电感 L m 增加——串联谐振的频移是增加质量的敏感指标,小于 1ng/cm 2 的薄膜可以很容易地通过 QCM 分辨出来。运动电阻 R m也可以提供有关该过程的重要变量,因为软薄膜和粘性液体会增加运动损耗,从而增加 R m 的值。
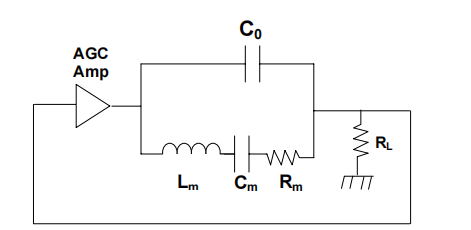
图 2.振荡器电路由 AGC 放大器、石英电阻器和负载电阻器组成。
将晶体放置在振荡器电路中提供了一种测量其运动参数的简单方法5 。图 2 显示了 BVD 晶体模型,由自动增益控制放大器驱动(AGC),且端接负载电阻 R L 。通过将 R L 上的电压返回到 AGC 放大器的输入端,如果有足够的增益,电路将以环路周围相移为 0°(或 360°的整数倍)的频率振荡(Barkhausen准则)。如果没有C o ,则很容易看出在C m 和L m 的串联谐振是(即f SR = [ 1 / [2.Π .(L m .C m )1/2 ])满足相位条件.在串联谐振时,C m 和 L m 的电抗抵消,只留下 R m 。在这种情况下,一个值为 A v =(R m + R L )/ R L 的放大器增益将提供 1 的环路增益来维持振荡。
不幸的是,C o 在 QCM 应用中不能被忽略。在图 2 所示的电路中,C o 向 R L 注入超前电流,该超前电流必须通过运动臂被滞后电流抵消,以达到零相位条件。这需要电路运行在串联谐振至上,其中C m 和 L m 的净电抗是感应的。事实上,如果 R m 足够大,运动臂可能无法提供足够的滞后电流来抵消通过 C o 的超前电流,电路也可能根本不会振荡。
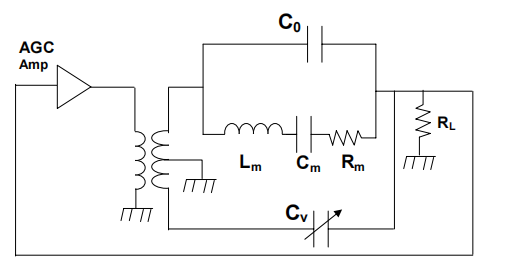
图 3.C 0 变零的振荡器电路。
图 3 显示了一种取消 C o 的方法。在这个电路中,AGC 放大器驱动具有两个次级绕组的变压器。一个次级驱动晶体和负载像以前一样,而另一个则是次级反转电压。反转电压源通过可调电容器 C v注入电流,以抵消通过 C o 注入的电流。当可调电容等于 C o 时,可以实现精确的抵消。在 SRS 的QCM25晶体控制器中,C v 是一个变容器,通过找到维持振荡所需增益*小的偏置设置,使其等于C o 。
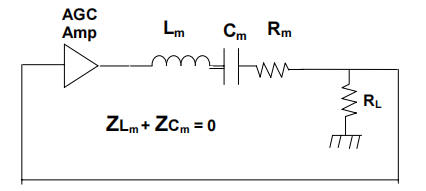
图 4.用 C v 抵消 C 0 的振荡器电路模型。
在 C o 取消后,电路简化为如图 4 所示。对于该电路,在 C m 和 L m 的电抗抵消的串联谐振中实现了零相位条件。在串联谐振时,R m 和 R L 形成一个电阻衰减器,需要 AGC 增益 A v =(R m + R L )/ R L来维持振荡。通过了解维持振荡所需的 AGC 增益6 A v ,我们可以确定 R m = R L .(A v - 1)。

北京卓立汉光仪器有限公司
仪器网(yiqi.com)--仪器行业网络宣传传媒