俯视法测量接触角的原理

俯视法接触角测量技术是基于对Laplace-Young模型的深刻理解和准确的运用。早在19世纪初Young和Laplace先后发表了二篇有关表面张力现象和本质的文章，把表面张力与表面二侧的压力差和表面的曲率半径联系起来：

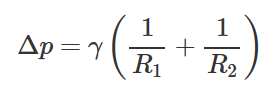
方程中Δp为表面两侧压力差

γ为表面张力

R1和R2为液滴表面正交方向的曲率半径

但是这个看似简单的方程在一般情况下无法求解，直到1882年Bashforth 和Adams把ZX轴对称前提引入Laplace-Young方程推导出了描述处于表面张力和重力平衡时的液滴轮廓的积分方程式：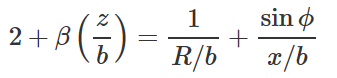                             

其中：                                  

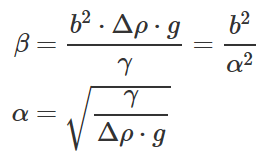
β又称为形状因子

α又称为毛细管常数

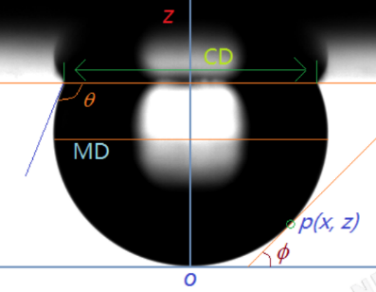
方程中b为液滴底端O处的曲率半径，可以根据液滴体积和CD值两个边界条件确定

R 为座滴轮廓上一点P（x,z）在纸平面上的主曲率半径

ϕ为轮廓线上点P（x,z）处的切线与X轴的夹角

Δρ 为液滴相与周围相之间的密度差

g 为重力加速度

γ为表面/界面张力

受益于二十世纪末计算机速度的大幅提高和高分辨率数码相机的出现，使得我们对图像数据求解上述方程成为了可能。

简单地说，在已知液体表面张力和密度的前提下，如果我们能够控制液滴的体积并且极ng确的测量液滴和材料表面三相接触线的形状尺寸，我们就可以利用Laplace-Young模型计算出液滴的三维轮廓，从而准确的得到接触角数值。